„Risikoaggregation, eine Methode zur Zusammenfassung quantitativ bewerteter Einzelrisiken zu einem erwartbaren Gesamtrisikoumfang.“
Quantitativ bewertete Einzelrisiken sind Risiken welche durch mindestens zwei Eigenschaften näher beschrieben sind, zum einen der Eintrittswahrscheinlichkeit und zum anderen der Schadenshöhe. Betrachtet man ein einzelnes Risiko isoliert, so lässt sich erkennen welcher Schaden mit welcher Wahrscheinlichkeit eintreten könnte, allerdings eben nur isoliert für dieses einzelne Risiko. Existiert eine größere Menge an Risiken, ist dies nicht mehr erkennbar, da die Betrachtung aller Einzelrisiken keinerlei Aussage über den Gesamtrisikoumfang liefert. Eine einfache Methode aus mehreren Risiken ein zu erwartendes Gesamtrisiko zu ermitteln, existiert nicht.
Einzelrisiken sind nicht zu einem Gesamtrisiko addierbar, auch wenn es Ansätze gibt, dies beispielsweise mit der Erwartungswertmethode zu tun. Näheres hierzu in unserem Vergleich der Erwartungswertmethode mit der Risikoaggregation: Methoden der Risikozusammenfassung
Würde man beispielsweise alle Schadenshöhen addieren, würde man voraussetzen, dass alle Risiken gleichzeitig eintreten. Der daraus resultierende Gesamtschaden würde eine der unwahrscheinlichsten Konstellationen widerspiegeln und es würde von einer eher unrealistischen Gesamtschadenshöhe ausgegangen werden. Der ebenfalls sehr unwahrscheinliche Fall, dass keines der Risiken eintritt würde zu einer Gesamtschadenshöhe von 0 führen, eine ebenso sehr unwahrscheinliche Konstellation. Die Wahrheit, bzw. die wahrscheinlichsten Fälle liegen dazwischen.
Vorgehensweise
Die vorherigen zwei Beispiele beschreiben sehr gut die Methodik der Risikoaggregation. Sie versucht herauszufinden, welche Konstellationen denn überhaupt und mit welcher Wahrscheinlichkeit eintreten können. Hierzu wird die Monte-Carlo-Simulation (Monte-Carlo-Methode – Ein Weg aus der Unsicherheit) zu Hilfe genommen, welche auf dem Gesetz der großen Zahlen aufbaut. D. h. es wird in endlich vielen Fällen simuliert, welche Konstellationen der Einzelrisiken zueinander eintreten können. Im Folgenden ist dies detaillierter mit 3 Fällen und einer Teilmenge aller Risiken dargestellt.
Fall 1
| Risiko | Eintrittswahrscheinlichkeit | Schadenshöhe | Eintritt | Schaden |
|---|---|---|---|---|
| Risiko 1 | 5 % | 1.000.000 € | Ja | 1.000.000 € |
| Risiko 2 | 75 % | 5.000.000 € | Nein | 0 € |
| Risiko 3 | 50 % | 2.000.000 € | Nein | 0 € |
| Risiko 4 | 15 % | 8.000.000 € | Nein | 0 € |
| … | … | … | … | … |
| Summe | 38.356.000 € |
Fall 2
| Risiko | Eintrittswahrscheinlichkeit | Schadenshöhe | Eintritt | Schaden |
|---|---|---|---|---|
| Risiko 1 | 5 % | 1.000.000 € | Ja | 1.000.000 € |
| Risiko 2 | 75 % | 5.000.000 € | Nein | 0 € |
| Risiko 3 | 50 % | 2.000.000 € | Ja | 2.000.000 € |
| Risiko 4 | 15 % | 8.000.000 € | Nein | 0 € |
| … | … | … | … | … |
| Summe | 60.656.000 € |
Fall 3
| Risiko | Eintrittswahrscheinlichkeit | Schadenshöhe | Eintritt | Schaden |
|---|---|---|---|---|
| Risiko 1 | 5 % | 1.000.000 € | Nein | 0 € |
| Risiko 2 | 75 % | 5.000.000 € | Ja | 5.000.000 € |
| Risiko 3 | 50 % | 2.000.000 € | Ja | 2.000.000 € |
| Risiko 4 | 15 % | 8.000.000 € | Ja | 8.000.000 € |
| … | … | … | … | … |
| Summe | 46.384.000 € |
Um ein möglichst genaues Bild der Konstellationen zu erhalten, sollte dieses Vorgehen in mindestens 100.000 Simulationsläufen wiederholt werden.
Am Ende des gesamten Simulationslaufes lässt sich erkennen, welche Konstellationen der einzelnen Risiken untereinander eintreten können und vor allem lässt sich erkennen, dass bestimmte Schadenshöhen oder Bereiche von Schadenshöhen häufiger eintreten als andere.
Im Folgenden sind alle eingetretenen Schadenshöhen mit ihrer jeweiligen Eintrittshäufigkeit dargestellt:
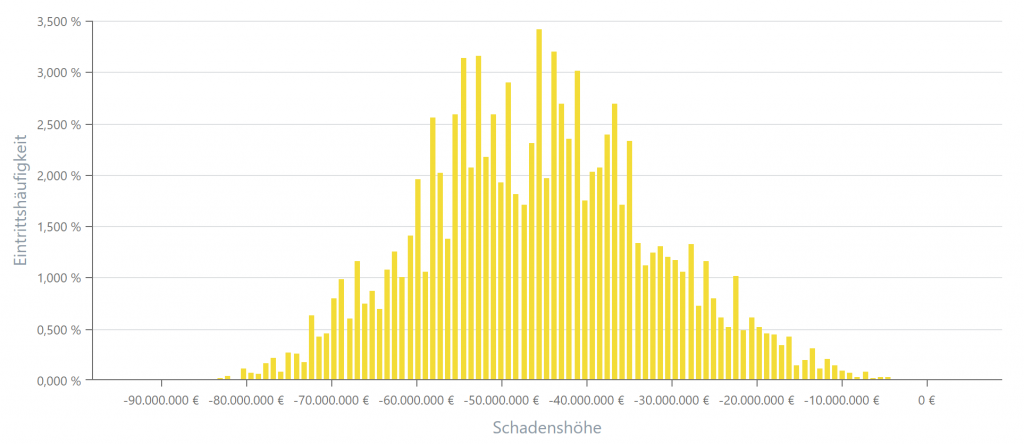
Über eine Analyse der einzelnen Simulationsläufe lässt sich somit ermitteln, welche Schadenshöhen mit welchen Wahrscheinlichkeiten eintreten können. Es lässt sich ganz klar erkennen, dass es wahrscheinlichere Konstellationen/Schadenshöhen gibt und unwahrscheinlichere. Die beiden aufgeführten Extrembeispiele zu Anfang (Eintritt aller Risiken gleichzeitig, Eintritt keines der Risiken) sind ganz klar als sehr unwahrscheinlich einzustufen. Werden die Simulationsläufe in einem weiteren Schritt entsprechend ihrer Schadenshöhen und der Eintrittswahrscheinlichkeit analysiert, lässt sich erkennen, mit welcher Wahrscheinlichkeit bestimmte Gesamtschadenshöhen zu erwarten sind.
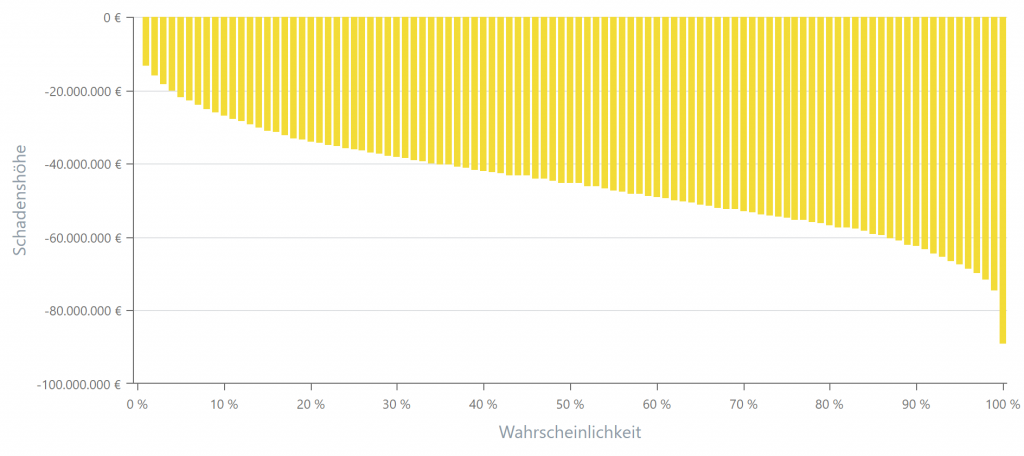
Es lässt sich sehr einfach der theoretisch minimal und der theoretisch maximal mögliche Schaden erkennen, ebenso wie die Entwicklung der Schadenshöhe in Bezug zur betrachteten Menge der Simulationsläufe. Des Weiteren lässt sich sehr einfach erkennen, in wie vielen Fällen eine bestimmte Schadenshöhe nicht überschritten wird. Beispielsweise wird im obigen Beispiel in 95 % aller Fälle eine Gesamtschadenshöhe von 67.400.000 € nicht überschritten.
In Verbindung mit Zeiteinheiten (beispielsweise Jahren) könnte nun die Aussage getroffen werden, dass obige Konstellation bedeutet:
Bei Betrachtung von 95 % aller Fälle wird ein Schaden in Höhe von 67.400.000 € nicht überschritten; ein höherer Schaden ist nur in 5 % aller Fälle, also etwa alle 20 Jahre zu erwarten.
Anwendungsgebiete
Risikoaggregation unter Anwendung der Monte-Carlo-Methode lässt sich in allen Bereichen einsetzen, in welchen mit unsicheren Werten gearbeitet wird und Risiken und Chancen existieren, welche auf diese Werte Einfluss nehmen. Voraussetzung ist die Vollständigkeit der wirkenden Risiken und Chancen und die quantitative Bewertungsmöglichkeit. Alle Risiken und Chancen müssen mit einer Wahrscheinlichkeit und einem möglichen Verlust oder Gewinn bewertet sein oder bewertet werden können. Der Verlust oder Gewinn kann hierbei als Einzelwert oder mit gängigen Verteilungsfunktionen festgelegt werden.
Sind diese Voraussetzungen gegeben, sind beispielsweise folgende Anwendungsgebiete möglich:
- erweiterte Unternehmensplanung unter Einbezug des Risikomanagements
- unternehmensweite Risikoaggregation zur Ermittlung der Risikotragfähigkeit für die Erfüllung des IDW PS 340 n. F. (2020), des StaRUG oder des DIIR Revisionsstandard Nr. 2
- Kalkulation von Investitionsprojekten, siehe hierzu auch Risikosimulation in Investitionsprojekten
- Kalkulation von Entwicklungs- oder Kundenprojekten
Fazit
Die Risikoaggregation erlaubt es, die Auswirkung quantitativ bewerteter Risiken genauer zu interpretieren. Sie liefert allerdings nicht eine zu erwartende Gesamtschadenshöhe, sondern sie liefert vielmehr die Wahrscheinlichkeiten mit welcher bestimmte Schadenshöhen eintreten bzw. nicht überschritten werden. Des Weiteren lässt die Risikoaggregation bei detaillierten Simulationsläufen und entsprechender Interpretation dieser auch Rückschlüsse auf die kritischsten Risiken zu, d. h. die Risiken, welche den größten Einfluss auf die entstehenden Gesamtschadenshöhen haben.
Interesse an Risikoaggregation?
Risikoaggregation über eine größere Menge an Risiken und mit ausreichend vielen Simulationsläufen ist nicht ohne spezielle Softwareunterstützung möglich. Hierfür kann beispielsweise unsere speziell dafür entwickelte Lösung RiskBoards eingesetzt werden. Für nähere Informationen hierzu sprechen Sie uns bitte an (Kontakt).