Risiken zu bewerten und mit ihnen umzugehen wird immer wichtiger. Sei es im Management des Unternehmens oder auch nur im Zuge eines definierten Projektes. Risiken bedrohen immer öfter gesamte Unternehmen oder führen zum Scheitern von Projekten, daher ist es wichtig so umfassend wie möglich negative Folgen aus bekannten Risiken zu vermeiden. Letztlich werden sich aber nicht alle Risiken vermeiden lassen und müssen dementsprechend als Bedrohung betrachtet und begrenzt auch akzeptiert werden. Doch wie werden diese nicht vermeidbaren Risiken bewertet? Wie kann ermittelt werden, mit welchem maximalen Schaden im schlimmsten Fall zu rechnen ist und zwar nicht mit Blick auf die einzelnen Risiken für sich, sondern mit Blick auf die Risiken in ihrer Gesamtheit.
Im Vorfeld der Risikobetrachtung ist viel Arbeit notwendig, um überhaupt Risiken zu identifizieren und genau analysieren zu können. Werden Risiken identifiziert, können sie grundsätzlich mit zwei Größen beschrieben werden:
Eintrittswahrscheinlichkeit
Wie groß ist die Wahrscheinlichkeit, dass das betrachtete Risiko eintritt? Im besten Fall kann zur Ermittlung dieser Größe auf Vergangenheits- oder Erfahrungswerte zurückgegriffen werden.
Schadenshöhe
Wie hoch ist der finanzielle Schaden, mit welchem bei Eintritt gerechnet werden muss? Auch hier ist es oftmals schwierig, konkrete Zahlen zu nennen. Im besten Fall kann aber auch hier auf Vergangenheits- oder Erfahrungswerte zurückgegriffen werden. Oftmals kann hier nicht die Festlegung auf einen Wert erfolgen, sondern es sollte mit Bereichen (von – bis) gearbeitet werden.
Doch wie ist mit den beiden ermittelten Werten, der Eintrittswahrscheinlichkeit und der Schadenshöhe nun zu verfahren? Welcher mögliche Schaden lässt sich daraus ableiten, bei einem, zwei oder beliebig vielen Risiken welche existieren. Zwei Ansätze sind die im Folgenden näher beschriebenen Methoden, zum einen die Erwartungswertbetrachtung und zum anderen die Risikoaggregation über eine Monte-Carlo Simulation.
Detailliertere Informationen zur Risikoaggregation über eine Monte-Carlo Simulation finden Sie auch in unserem Beitrag Risikoaggregation mit der Monte-Carlo-Methode.
Erwartungswertbetrachtung
Die Erwartungswertbetrachtung versucht aus den Mittelwerten einzelner Ereigniseintritte einen Gesamtwert zu ermitteln. Mit Blick auf Risiken wird hierbei der mittlere Schaden, welcher durch ein Risiko entsteht, folgendermaßen errechnet:
Eintrittswahrscheinlichkeit X Schadenshöhe = Erwartungswert
Konkret würde dies in einem Beispiel bedeuten:
Für ein Unternehmen besteht das Risiko des Ausfalles einer Maschine. Betrachtet wird hierbei nur der entstehende Schaden, welcher für eine Neuanschaffung entsteht. Dieser Schaden beläuft sich auf 125.000 €. Der Ausfall der Maschine wird mit einer Eintrittswahrscheinlichkeit von 5 % bewertet. Somit ergibt sich folgender Erwartungswert für den eintretenden Schaden.
5 % * 125.000 € = 6.250 €
Dies bedeutet, dass der zu erwartende Schaden bei 6.250 € liegt, unter Beachtung der Schadenshöhe und der Wahrscheinlichkeit mit welcher der Schaden eintreten kann.
Bei Betrachtung mehrerer Risiken könnte sich folgendes Bild ergeben:
| Risiko | Eintrittswahrscheinlichkeit | Schadenshöhe | Erwartungswert |
|---|---|---|---|
| Ausfall/Ersatz Maschine A | 5% | 125.000 € | 6.250 € |
| Ausfall/Ersatz Maschine B | 10% | 75.000 € | 7.500 € |
| Einsturz Hallendach Lager 1 | 2% | 85.000 € | 1.700 € |
| Wegfall Kunde A | 15% | 190.000 € | 28.500 € |
Doch wie lässt sich jetzt der zu erwartende Gesamtschaden ermitteln? Bei der Erwartungswertbetrachtung erfolgt dies durch eine einfache Addition der ermittelten, einzelnen Erwartungswerte.
| Risiko | Eintrittswahrscheinlichkeit | Schadenshöhe | Erwartungswert |
|---|---|---|---|
| Ausfall/Ersatz Maschine A | 5% | 125.000 € | 6.250 € |
| Ausfall/Ersatz Maschine B | 10% | 75.000 € | 7.500 € |
| Einsturz Hallendach Lager 1 | 2% | 85.000 € | 1.700 € |
| Wegfall Kunde A | 15% | 190.000 € | 28.500 € |
| Summe | 43.950 € |
Dies bedeutet, dass bei Betrachtung aller Risiken unter Beachtung deren Schadenshöhe und der jeweiligen Wahrscheinlichkeit mit einem möglichen Gesamtschaden von 43.950 € gerechnet werden muss.
Die Ermittlung von zu erwartenden Schäden durch Risiken anhand der Erwartungswertbetrachtung ist einfach und nachvollziehbar machbar. Allerdings wird auch sehr schnell deutlich, dass sie nur sehr begrenzte Aussagekraft hat. Schon bei Betrachtung eines einzelnen Risikos und des errechneten Erwartungswerts wird deutlich, dass, sollte ein Risiko wirklich eintreten, der ermittelte durchschnittliche Schadenswert bei weitem nicht ausreicht, um das Risiko im Ernstfall tragen zu können. Bei Betrachtung aller Risiken in Ihrer Gesamtheit und dem ermittelten Gesamtrisiko vervielfacht sich diese Problematik.
Risikoaggregation mit der Monte-Carlo-Simulation
Die Monte-Carlo-Simulation ist ein Verfahren aus der Stochastik, welches versucht durch eine große Anzahl von Zufallsexperimenten eine mathematisch schwere Aufgabenstellung zu lösen bzw. zu interpretieren. Sie basiert auf dem Gesetz der großen Zahlen und besagt, dass mit zunehmender Anzahl an Iterationen die Abweichung vom Erwartungswert gegen Null konvergiert.
Für die Risikoaggregation bedeutet dies, dass das Eintreten aller Risiken mit Ihrer Eintrittswahrscheinlichkeit und ihrer Schadenshöhe in sehr vielen Durchläufen simuliert wird, um am Ende eine Aussage treffen zu können, wie hoch der zu erwartende Gesamtschaden sein könnte.
Im Detail betrachtet wird in einem Durchgang für jedes Risiko durch ein Zufallsexperiment ermittelt, ob dieses Risiko eintritt oder nicht. Tritt es ein, entsteht der angegebene Schaden in voller Höhe. Tritt das Risiko nicht ein, entsteht kein Schaden. Treten mehrere Risiken in einem Durchgang ein, so werden diese Schäden summiert. Ausschlaggebend für den Eintritt ist die definierte Eintrittswahrscheinlichkeit des entsprechenden Risikos.
Im Folgenden ist dies anhand eines Beispiels detailliert dargestellt:
Durchgang 1
| Risiko | Eintrittswahrscheinlichkeit | Schadenshöhe | Eintritt | Schaden |
|---|---|---|---|---|
| Ausfall/Ersatz Maschine A | 5% | 125.000 € | Ja | 125.000 € |
| Ausfall/Ersatz Maschine B | 10% | 75.000 € | Nein | 0 € |
| Einsturz Hallendach Lager 1 | 2% | 85.000 € | Nein | 0 € |
| Wegfall Kunde A | 15% | 190.000 € | Nein | 0 € |
| Summe | 125.000 € |
Durchgang 2
| Risiko | Eintrittswahrscheinlichkeit | Schadenshöhe | Eintritt | Schaden |
|---|---|---|---|---|
| Ausfall/Ersatz Maschine A | 5% | 125.000 € | Nein | 0 € |
| Ausfall/Ersatz Maschine B | 10% | 75.000 € | Ja | 75.000 € |
| Einsturz Hallendach Lager 1 | 2% | 85.000 € | Ja | 85.000 € |
| Wegfall Kunde A | 15% | 190.000 € | Nein | 0 € |
| Summe | 160.000 € |
Durchgang 3
| Risiko | Eintrittswahrscheinlichkeit | Schadenshöhe | Eintritt | |
|---|---|---|---|---|
| Ausfall/Ersatz Maschine A | 5% | 125.000 € | Nein | 0 € |
| Ausfall/Ersatz Maschine B | 10% | 75.000 € | Nein | 0 € |
| Einsturz Hallendach Lager 1 | 2% | 85.000 € | Nein | 0 € |
| Wegfall Kunde A | 15% | 190.000 € | Nein | 0 € |
| Summe | 0 € |
Durchgang n
| Risiko | Eintrittswahrscheinlichkeit | Schadenshöhe | Eintritt | Schaden |
|---|---|---|---|---|
| Ausfall/Ersatz Maschine A | 5% | 125.000 € | Nein | 0 € |
| Ausfall/Ersatz Maschine B | 10% | 75.000 € | Ja | 75.000 € |
| Einsturz Hallendach Lager 1 | 2% | 85.000 € | Nein | 0 € |
| Wegfall Kunde A | 15% | 190.000 € | Nein | 0 € |
| Summe | 75.000 € |
Dieses Vorgehen wird in einer sehr großen Anzahl von Durchgängen (ca. 100.000) wiederholt. Im Anschluss daran werden die einzelnen Durchgänge analysiert in Bezug auf Ihre simulierte Schadenshöhe und die entsprechende Eintrittshäufigkeit, um hieraus schlussfolgern zu können mit welchem Schaden mit welcher Wahrscheinlichkeit zu rechnen ist.
Für das dargestellte Beispiel ergibt sich aus 100.000 Simulationsläufen die folgende Verteilung:
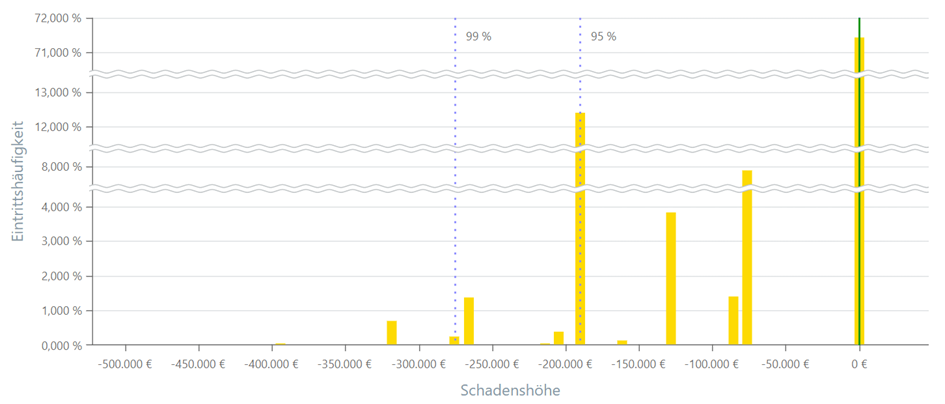
In ca. 71,5 % der Fälle ist keines der definierten Risiken eingetreten und somit kein Schaden entstanden. In den übrigen Fällen sind mit der dargestellten Eintrittshäufigkeit Schäden in angegebener Höhe eingetreten. Die eingetretenen Schäden belaufen sich auf 75.000 € bis 475.000 €.
Bei Betrachtung aller Risiken und aller Simulationsläufe der Monte-Carlo-Simulation ergibt sich für obiges Beispiel bei 28,5 % aller Fälle ein Schaden und zwar in Höhe von mindestens 75.000 €.
Die Risikoaggregation mit Hilfe der Monte-Carlo-Simulation ist nicht ohne spezielle Software oder Softwaremodule durchführbar. Das Vorgehen zur Erreichung aussagekräftiger Ergebnisse ist komplexer und umfangreicher als mit der Erwartungswertbetrachtung. Allerdings bietet diese Methode auch viele Möglichkeiten den Umgang mit Risiken und deren Bewertung noch detaillierter anzugehen. Beispielsweise ist es in vielen Fällen sinnvoll, nicht mit festen Schadenshöhen zu arbeiten, sondern mit Verteilungsfunktionen. Gängige Verteilungsfunktionen wären hierbei z. B.:
- Gleichverteilung
- Dreiecksverteilung
- Normalverteilung
Mit Nutzung dieser Verteilungen können beispielsweise Ungenauigkeiten in der Risikobewertung abgemildert werden. Eine feste Schadenshöhe von 75.000 € würde dann z. B. bei Verwendung einer Gleichverteilung als Bereich definiert werden zwischen 60.000 € und 90.000 €. Im Zuge der Monte-Carlo Simulation wird bei Simulation dieses Risikos dann über ein Zufallsexperiment ermittelt, welche Schadenshöhe aus diesem Bereich auftritt, sofern das Risiko eintreten würde.
Fazit
Im Vergleich zur Erwartungswertbetrachtung ist die Aggregation über eine Monte-Carlo Simulation weitaus umfangreicher und komplexer, mit entsprechender Softwareunterstützung aber problemlos umsetzbar. Eine Risikoaggregation bildet zu erwartende Schadenshöhen durch die Vielzahl an Simulationsläufen wahrheitsgetreuer ab als eine einfache Erwartungswertbetrachtung. Mit obigen Beispielen wäre der zu erwartende Schaden bei der Erwartungswertbetrachtung bei 43.950 € gelegen, was weniger ist als der Schaden des geringsten Risikos wenn es eintreten würde. Somit wird deutlich welche Ungenauigkeit diese Methode liefert. Bei der Risikoaggregation hingegen ist die Aussage die, dass in mind. 28,5 % aller Fälle mit einem Schaden von mindestens 75.000 € zu rechnen ist. Hiermit wird deutlich, dass die Risikoaggregation die weitaus nachvollziehbareren Folgerungen zulässt.
Informationen zur Risikosimulation und Risikoaggregation mit unserer Lösung RiskBoards finden Sie hier: RiskBoards – Risikosimulation und Aggregation