Wahrscheinlichkeitsverteilungen sind mathematische Modelle, die die Wahrscheinlichkeiten verschiedener Ereignisse oder Ausprägungen einer Zufallsvariablen beschreiben. Sie spielen eine zentrale Rolle in der Wahrscheinlichkeitstheorie und Statistik.
Im Folgenden sind einige Informationen zu Wahrscheinlichkeitsverteilungen aufgeführt, welche häufig – beispielsweise auch in der Risikoaggregation – Verwendung finden:
Verteilungsfunktionen
Normalverteilung (auch Gauss-Verteilung genannt)
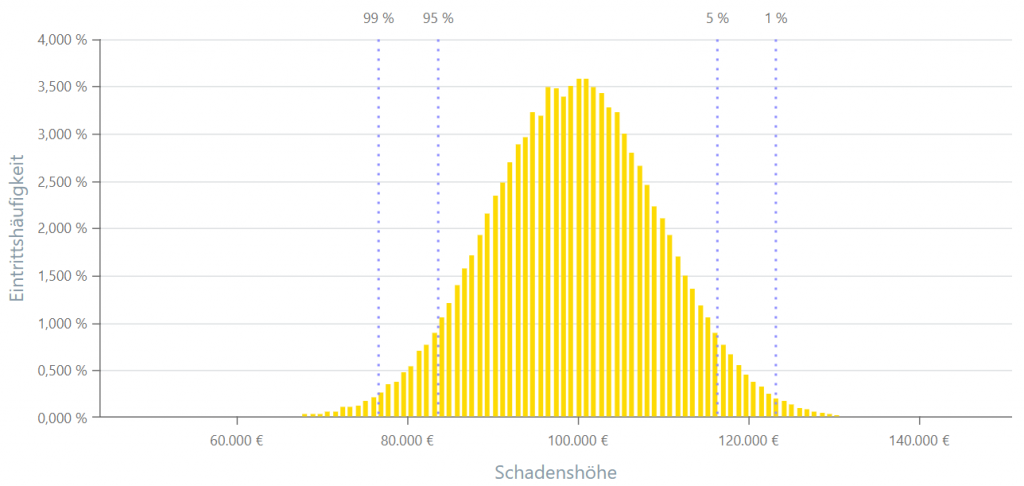
Die Normalverteilung ist eine der bekanntesten Wahrscheinlichkeitsverteilungen. Sie ist durch ihre charakteristische glockenförmige Kurve gekennzeichnet. In einer Normalverteilung ist der Mittelwert das Zentrum der Verteilung, während die Standardabweichung die Breite steuert. Viele natürliche Phänomene und Messungen nähern sich einer Normalverteilung an, was die Bedeutung dieser Verteilung in der Statistik erklärt.
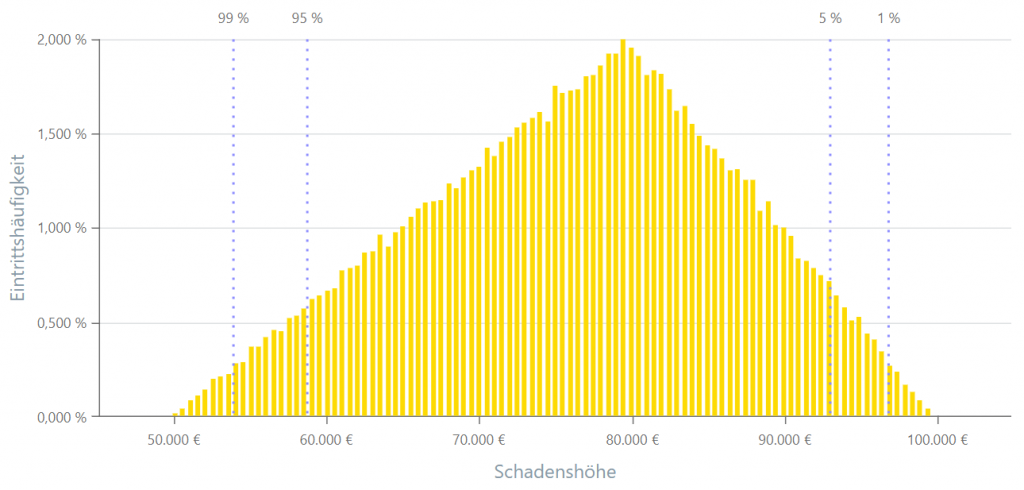
Dreiecksverteilung
Die Dreiecksverteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung, bei der die Wahrscheinlichkeitsdichte eine dreiecksförmige Form aufweist. Sie wird häufig verwendet, wenn über die Verteilung einer Zufallsvariable nur begrenzte Informationen verfügbar sind. Die Verteilung wird durch drei Parameter definiert: den minimalen Wert, den maximalen Wert und den Modus (den wahrscheinlichsten Wert).
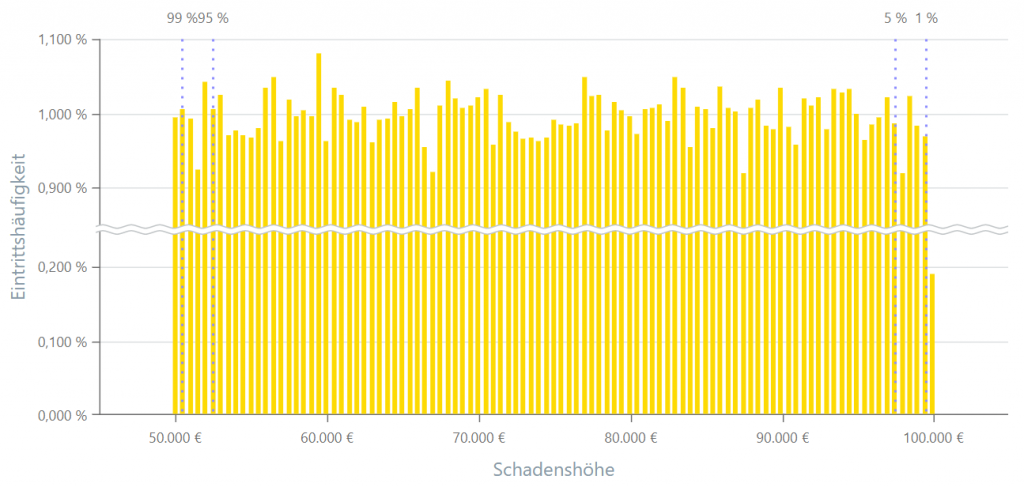
Gleichverteilung
Die Gleichverteilung, auch Rechteckverteilung genannt, ist eine Wahrscheinlichkeitsverteilung, bei der alle Ausprägungen innerhalb eines bestimmten Intervalls die gleiche Wahrscheinlichkeit haben. Es gibt diskrete und kontinuierliche Gleichverteilungen. Bei der diskreten Gleichverteilung sind alle möglichen Werte gleich wahrscheinlich, während bei der kontinuierlichen Gleichverteilung die Wahrscheinlichkeitsdichte konstant ist.
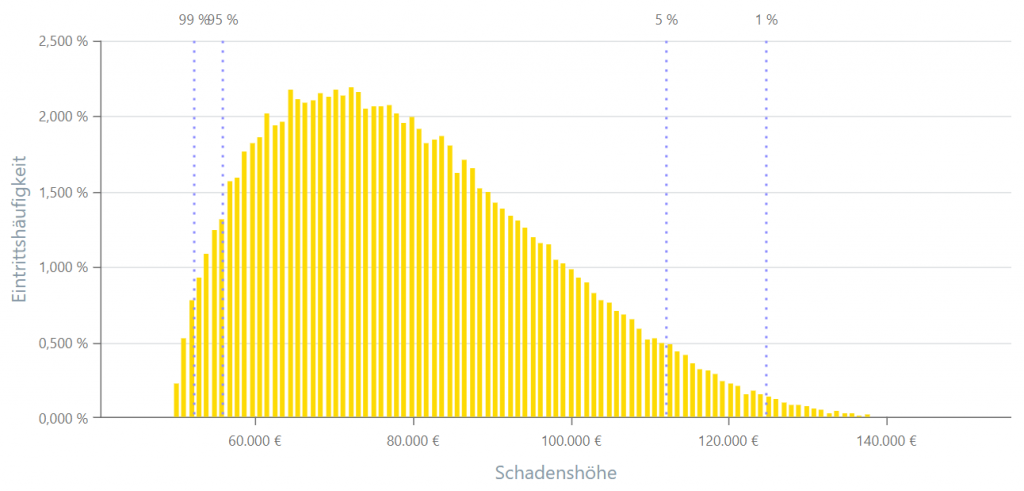
PERT-Verteilung
Die PERT-Verteilung, abgeleitet von „Program Evaluation and Review Technique“, ist eine Wahrscheinlichkeitsverteilung, die oft in Projektmanagement und Risikoanalyse verwendet wird. Sie modelliert unsichere Parameter, indem sie den minimalen, wahrscheinlichen und maximalen Wert der Verteilung berücksichtigt. Die PERT-Verteilung ähnelt einer Dreiecksverteilung, auch bei dieser definiert der Modus die wahrscheinlicheren Werte.
Trapezverteilung
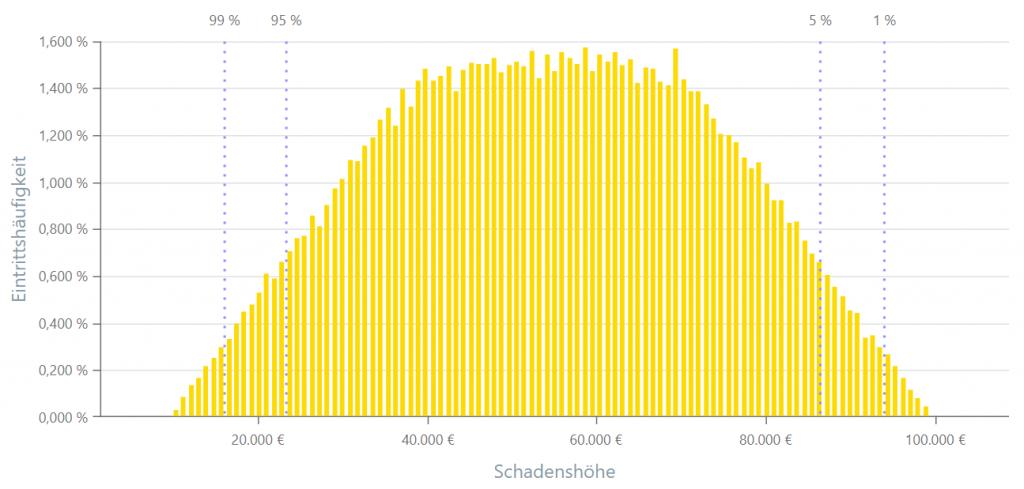
Die Trapezverteilung ist eine Wahrscheinlichkeitsverteilung, bei der die Wahrscheinlichkeitsdichte eine trapezförmige Form aufweist. Sie wird verwendet, um die Unsicherheit um einen Wert herum zu modellieren, wenn nur begrenzte Informationen zur Verteilung verfügbar sind. Die Verteilung wird durch vier Parameter definiert: den minimalen Wert, den linken Modus, den rechten Modus und den maximalen Wert.
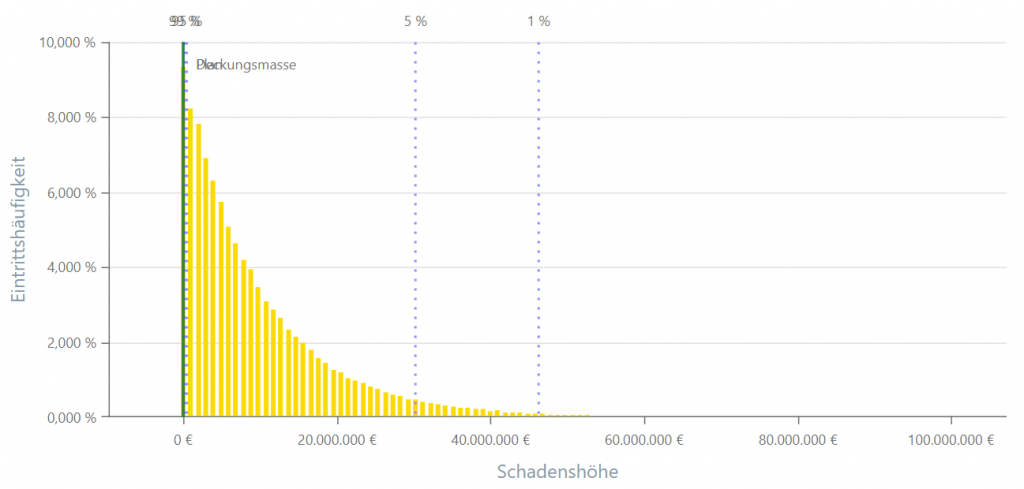
Exponentialverteilung
Die Exponentialverteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung, die oft zur Modellierung von Wartezeiten oder Zeitspannen zwischen Ereignissen verwendet wird. Sie ist durch eine abnehmende Exponentialfunktion gekennzeichnet
Dies sind nur einige Beispiele von Wahrscheinlichkeitsverteilungen. Es gibt viele weitere Verteilungen mit unterschiedlichen Eigenschaften und Anwendungen, die in der Statistik und Wahrscheinlichkeitstheorie verwendet werden.
Welche Verteilungsfunktion für welchen Fall?
Die Wahl der richtigen Verteilungsfunktion ist wichtig aus mehreren Gründen:
- Realistische Modellierung:
Durch die Auswahl einer geeigneten Verteilungsfunktion kann ein realistisches Modell für die zugrunde liegenden Daten oder Variablen geschaffen werden. Unterschiedliche Verteilungen haben unterschiedliche Formen und Eigenschaften, die zu verschiedenen Phänomenen passen. Wenn die gewählte Verteilungsfunktion nicht zur Natur der Daten passt, kann das Modell fehlerhaft sein und unzuverlässige Ergebnisse liefern. - Parameterabschätzung:
Verteilungsfunktionen haben oft Parameter, die bestimmte Eigenschaften der Verteilung steuern, wie zum Beispiel den Mittelwert oder die Standardabweichung. Durch die Wahl der richtigen Verteilungsfunktion können diese Parameter genauer geschätzt werden, was zu einer besseren Modellanpassung führt. - Vorhersagegenauigkeit:
Wenn die Verteilungsfunktion gut zur zugrunde liegenden Verteilung passt, kann sie verwendet werden, um Vorhersagen über zukünftige Ereignisse oder Variablen zu machen. Eine falsche Wahl der Verteilungsfunktion kann zu ungenauen Vorhersagen führen und das Vertrauen in die Modellergebnisse beeinträchtigen.
Fazit
Es ist wichtig anzumerken, dass die Wahl der Verteilungsfunktion nicht immer eindeutig ist und von verschiedenen Faktoren abhängt, wie dem vorhandenen Wissen über das Phänomen, der Verfügbarkeit von Daten und der spezifischen Anwendungsdomäne. In einigen Fällen kann es auch sinnvoll sein, empirische Verteilungen zu verwenden, die direkt aus den beobachteten Daten abgeleitet werden, wenn keine geeignete theoretische Verteilung gefunden werden kann.